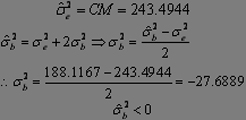Diseños experimentales - Modelos estadísticos
Efectos fijos vs. Efectos aleatorios 

M. Flores¹, E. Gonzáles²
1. Investigador ACECAP - Consultor Proyectos de Investigación - Estadística - Informática
2. Especialista Recursos Fitogenéticos y Biometría
E-mail: marcelo@agr.umss.edu.bo

Introducción

La estadística, como una herramienta de la investigación, provee de una serie de opciones y matices con la finalidad que los investigadores puedan hacer un acercamiento a la realidad de manera mas fiable. La pertinencia o no de una conclusión, como respuesta a un problema planteado, dependerá del uso adecuado de la herramienta, por tanto, esto implica que debemos tener cuidado en aspectos como el diseño experimental a utilizar y el modelo estadístico a proponer, entre otros.

Un diseño experimental es la forma en la cual el investigador aplica los efectos a ser estudiados a las unidades experimentales mediante tratamientos y una vez obtenidos los datos de campo, estos se analizan a través del modelo estadístico propuesto, que normalmente guarda relación con el diseño. Asimismo, los modelos estadísticos se componen de dos tipos de efectos, los fijos que son del interés del investigador y los aleatorios que siempre están presentes en todos los modelos utilizados en los diseños, razones por las cuales, actualmente se denominan modelos mixtos.

Objetivo del presente texto

Interpretar eficientemente las varianzas de los efectos aleatorios a fin de optimizar el uso de un modelo estadístico y su implicancia en los diseños experimentales.

Algunas definiciones importantes

Diseño experimental. El diseño experimental es una estrategia de combinación de la estructura de tratamientos (factores de interés) con la estructura de unidades experimentales, de manera tal que las alteraciones en las respuestas, al menos en algún subgrupo de unidades experimentales, puedan ser atribuidas solamente a la acción de los tratamientos, excepto por variaciones aleatorias.

Modelo. Las variables medidas o cuantificadas proveen datos a analizar, las que pueden provenir de ensayos realizados bajo diferentes diseños experimentales, sean estos completamente aleatorizados, bloques completos al azar, bloques incompletos balanceados, cuadrado latino, parcelas divididas, anidados etc. (Snedecor 1956; Ostie 1977; Di Rienzo et al., 2001).

Para poder obtener una solución de las ecuaciones normales para la estimación de los parámetros, se usa las restricciones usuales: suma de los efectos de distintos niveles de un factor igual a cero. Esta clase de restricciones, sobre los efectos de los factores en el modelo, tiene una interpretación sencilla si se definen los efectos de los niveles de los factores como desvíos con respecto a la media general. Al imponer esas restricciones, se obtienen soluciones para los parámetros fijos del modelo (Cochran y Cox 1957).

El Modelo Lineal Aditivo. La calidad de un análisis estadístico esta directamente relacionada con la adecuación del modelo que se asume para describir los datos. Un modelo debe representar adecuadamente la característica muestra! de los datos y reflejar el problema biológico. Hay tres niveles de modelos (Siles 2001).

• Modelo verdadero que describe los datos perfectamente, sin variación residual o no explicada. El modelo verdadero nunca es exactamente conocido.

• Un modelo ideal que es una formulación del experimentador, tan próxima al modelo verdadero como sea posible. El modelo ideal tendría que ser el modelo que se usara para el análisis pero a menudo no se tiene suficiente información disponible como para aplicarlo en la practica.

• Modelo operacional es una versión simplificada del modelo ideal, y es el que el experimentador usará en el análisis. A menudo no hay acuerdo entre los investigadores de cual es el mejor modelo operacional a utilizar.

Para elaborar un modelo operacional correcto, el experimentador debe construir un modelo ideal. Dadas las limitaciones de los datos y los recursos bajo los cuales debe funcionar el experimentador, el modelo operacional puede elaborarse simplificando apropiadamente el modelo ideal. Si se realizan demasiadas simplificaciones o se imponen demasiados supuestos, entonces puede ocurrir que el análisis no sea válido.

Los modelos contendrán un grupo de factores que afectan aditivamente al valor de la variable. Pero un modelo no solo es la expresión matemática o ecuación, sino el conjunto de supuestos, restricciones y limitaciones implícitas.

El modelo lineal aditivo, por tanto, trata de explicar una observación como una suma de componentes tales como la media paramétricas más unos elementos de variación aleatorios que pueden ser asociados a diferentes efectos, fuentes de variación o factores, más un error que incluirá tanto los errores de medida como los errores de muestreo y el error experimental.

Análisis de la varianza. El análisis de varianza (ANOVA del término ingles Analysis of Variance) es un procedimiento que descompone la variabilidad total en la muestra (suma de cuadrados total de las observaciones) en componentes (sumas de cuadrados) asociados cada uno a una fuente de variación reconocida (Nelder 1994; Searle 1971, 1987).

Se utiliza el nombre de análisis de la varianza ya que el elemento básico del análisis estadístico seria precisamente el estudio de la variabilidad.

En experimentos donde se realiza la aplicación de varios tratamientos, a un conjunto de unidades experimentales para medir y comparar las variables de respuesta, es imperioso administrar eficientemente los recursos que permitan incrementar la precisión de las estimaciones de las respuestas promedio de tratamientos y las comparaciones entre ellas. Se entiende por tratamientos a la/s acciones que se aplican sobre las unidades experimentales (parcelas, macetas, animales, cajas petri, etc.) y que son objeto de comparación.

La reducción del error o variabilidad entre unidades experimentales que reciben el mismo tratamiento, es uno de los principales objetivos de la planificación de un experimento, siguiendo un diseño experimental, con el propósito de incrementar precisión y sensibilidad al momento de la inferencia.

La evaluación de los efectos fijos dentro el ANVA, se realiza a través de una prueba de F y los efectos aleatorios mediante varianzas y covarianzas (Peña, 1994).

Cuando se observa un cuadro de ANVA, para el caso de un diseño BCAA, normalmente se muestra un valor de F calculado para bloques, que no corresponde, lo apropiado es medir la varianza entre bloques y determinar si hubo variación o no a partir de las Esperanzas de los Cuadrados Medios (ECM).

La pregunta es ¿sí no hubo variación entre bloques, cual es la implicancia en el diseño experimental?, la respuesta es simple, ninguna.

Para algunos la respuesta puede parecer no convincente, porque se pensaba que modificando el modelo era también necesario modificar el diseño, pero lo apropiado es tomar la decisión de cambiar el modelo, a partir de la absoluta seguridad que no hubo variación entre bloques y lo adecuado es eliminar este efecto en el modelo, dando como resultado un valor más preciso del F calculado para los efectos fijos estudiados. Ejemplo: ver estudio de caso.

Estudio de caso (modificado de Muñoz, 2002). Se ha medido la longitud del tórax de dos especies de chinche de las plantas, Halticus oleracea y Halticus carduorum. Los datos fueron levantados en bloques por la posición de los insectos en las plantas (superior e inferior). El modelo usado fue:

Y_ij = µ + ß_i + τ_j + ξ_ij

donde:

El análisis de varianza obtenido fue:

Testeando el modelo a partir de la ECM del procedimiento GLM (SAS®, 2000):
 

>>> la varianza entre bloques es menor a cero, lo cual significa que no hubo variación entre bloques, por tanto el diseño de bloques completos al azar, no fue eficiente para controlar la variación entre las diferentes unidades experimentales (UE).

Con esta información el investigador puede eliminar el efecto de bloques que inicialmente pensó que pudo influir. El nuevo cuadro de anva es el siguiente:

Donde los CM del error fueron afectados por los gl incrementados de 9 a 18, lo que repercute directamente en la precisión de estimación del F calculado para el efecto fijo, cuya probabilidad asociada varía de Pr = 0.0465 a 0.0247. Este proceso es corroborado por el procedimiento Mixed (SAS ®,2000) detallado al final del presente artículo.

Estimadores de parámetro de covarianza

Test de tipo 3 de efectos fijos

Referencias

COCHRAN, W., COX, G. 1957. Experimental Designs. John Wiley & Sons, Inc. London.

Di RIENZO, J., CASANOVES, F., GONZÁLEZ, L.,TABLADA, E., DÍAZ, M., ROBLEDO, C.,BALZARINI, M. 2001. Estadística para las Ciencias Agropecuarias. 4ta Ed. Triunfar. Córdoba, Argentina.

MUÑOZ, A. 2002. Estadística Aplicada Uni y Multivariante. Universidad de Córdoba. España.

NELDER, J. 1994. The Statistics of Linear Models: Back to Basics. Statistics and Computing. 4: 243- 256. In: lnfoStat (2004). lnfoStat, y. 2004. Manual del Usuario. Grupo InfoStat, FCA, Universidad Nacional de Córdoba. ira. ed. Argentina.

OSTLE, B. 1977. Estadística aplicada. Técnicas de la estadística moderna, cuando y donde aplicarlas. Ed. Limusa. México.

PEÑA, S. 1994. Estadística: modelos y métodos. 1. Alianza Universidad Textos. Madrid.

SAS Institute (System Analysis Statiscal). 200c Lenguaje and procedure. Usage. Versión 8, 1 ed. SAS Inst. Cary. NC.

SEARLE, 5. 1971’. Linear Models. New York, John Wiley & Sons, Inc., New York. In: lnfoStat (2004). lnfoStat, y. 2004. Manual del Usuario. Grupo lnfoStat, FCA, Universidad Nacional de Córdoba. ira. ed. Argentina.

SEARLE, 5. 1987. Linear Modeis for Unbalanced Data. New York, John Wiley & Sons, Inc., New York. In: InfoStat (2004). lnfoStat, y. 2004. Manual del Usuario. Grupo InfoStat, FCA, Universidad Nacional de Córdoba. Argentina.

SILES, M. 2001. Apuntes del curso “Estadística Avanzada para Investigadores”. Módulos I-II FCAyP - UMSS. 150 p.

SNEDECOR, G. 1956. Métodos Estadísticos Aplicados a la Investigación Agrícola y Biológica. México.

Corrida SAS ® del estudio de caso: