Diseño de bloques incompletos con una sola repetición
en la evaluación preliminar de material avanzado
en programas de mejoramiento genético de cultivos

M. Siles¹
1. Docente de Diseños Experimentales y Fitomejoramiento FCAyP - UMSS
Docente de Bioestadística, Carrera de Biología, FCyT - UMSS
Responsable del Programa de Mejoramiento Genético de Arveja, Centro de Investigaciones Fitoecogenéticas de Pairumani
E-mail: msiles@supernet.com.bo

En programas de mejoramiento de cultivos, se desarrollan grandes cantidades de genotipos, inicialmente con poca semilla o material vegetal que limita el uso de diseños experimentales con repeticiones. Debido a esta deficiencia, la presente investigación se llevo acabo con los objetivos de i) desarrollar un diseño experimental para evaluar preliminarmente material genético con una sola repetición y ii) determinar la eficiencia del diseño experimental propuesto. El diseño experimental consistió en la distribución de los nuevos genotipos en distintos bloques con una sola repetición, acompañados en cada bloque con tres o cuatro terceros genotipos (testigos) que hacen de referencia para estimar las varianzas entre bloques y residuales y los errores estándar y hacen posible la comparación entre genotipos distribuidos en el mismo o diferentes bloques y estos con los testigos. Los resultados de las evaluaciones de 174 y 132 líneas de arveja derivadas de dos distintas cruzas por rendimiento de grano, longitud de vaina, peso de 100 semillas, vigor e incidencia de oidiosis indican que el diseño experimental permite estimar las varianzas entre bloques y de los residuales, las cuales fueron importantes para ajustar las medias y comparar genotipos ubica dos en el mismo o distintos bloques y con los testigos. Asimismo, a pesar de las diferencias en los errores estándar, las comparaciones entre genotipos tuvieron aproximadamente el mismo nivel de precisión.

Introducción

En programas de mejoramiento genético de cultivos autógamas (arveja, cebada, frijol, soya, trigo, etc.) y de reproducción asexual (papa, caña de azúcar, etc) se desarrollan una gran cantidad de líneas y clones, respectivamente, con la finalidad de identificar los más sobresalientes. En especies alógamas, como el maíz, también se desarrollan un número grande de líneas, inicialmente con el objetivo de identificar las más apropiadas por su aptitud combinatoria general (ACG) y las combinaciones híbridas de estas con mejor aptitud combinatoria específica (ACE) (Fehr, 1993).

Las líneas desarrolladas en autógamas (F₄, F₅) y los clones en especies de reproducción asexual cuentan inicialmente con poca cantidad de semilla y material vegetal, respectivamente, que en la mayoría de los casos alcanza solo para un surco de uno a tres metros de largo, por ejemplo, en arveja solo es suficiente para un surco de un metro de largo. Bajo estas condiciones, las selecciones se basan simplemente en apreciaciones subjetivas, con el gran peligro de descartar algunos genotipos potenciales o para evitar este riesgo algunas veces primeramente se incrementa el material, aumentando más el tiempo en la obtención de una variedad. En otras situaciones, aún cuando se cuenta con suficiente cantidad de semilla, por ejemplo, algunas autógamas como cola de zorro (Setaria italica, (L.) Beauv) que de una sola planta se puede cosechar más de 6000000 semillas (Malm y Rachie, 1971), o en maíz, el híbrido que resulta de cada línea cruzada a un probador para evaluar por su ACG o los híbridos entre distintas líneas (simples, de tres vías o dobles) puede disponer de más de 1000 semillas (Fehr, 1993), debido a la gran cantidad de material resultante (por ejemplo, 4950 híbridos simples en base solo a 100 líneas), los ensayos se establecen con una sola repetición y las selecciones también son muy subjetivas y el peligro de descartar buenos genotipos persiste, aunque este riesgo podría reducirse de acuerdo a la experiencia del mejorador.

Las evaluaciones del material genético desarrollado se realizan mediante el uso de diferentes diseños experimentales, completamente aleatorio, bloques completos al azar, o filas y columnas. Con estos diseños se pueden evaluar una reducida cantidad de genotipos con al menos 2 repeticiones. Para el caso de un gran número de genotipos se han desarrollado los diseños de látices cuadrados y rectangulares. Sin embargo, al igual que los diseños elementales, requieren que los genotipos sean establecidos por lo menos con 2 repeticiones. Consecuentemente, estos diseños mencionados no serian apropiados para la evaluación del material genético desarrollado con una sola repetición. Lo cual sugiere la necesidad de buscar nuevas herramientas estadísticas que permitan evaluar apropiadamente la gran cantidad de mate-rial genético desarrollado, cuya semilla o material vegetal no es suficiente para más que una repetición o para aprovechar mejor aquellos ensayos que se establecen con una repetición. Por tanto, el presente trabajo de investigación tiene los objetivos de i) desarrollar un diseño experimental para evaluar material genético con una sola repetición y ii) determinar la eficiencia del diseño experimental propuesto.

Materiales y métodos

Desarrollo del diseño experimental

 Uno de los objetivos en todo proceso de mejoramiento de plantas es realizar comparaciones precisas entre distintos genotipos para seleccionar aquellos que expresen las características deseables. Dos genotipos pueden ser comparables cuando estos son evaluados en las mismas condiciones y es posible estimar el error estándar de la diferencia de sus medias. Considere el caso de 4 genotipos (A, B, C y D) distribuidos en distintas condiciones (bloques):

Bajo esta distribución, debido a que las condiciones son iguales, solo los genotipos distribuidos en el mismo bloque, A-B y C-D, pueden ser comparados, y no así entre genotipos que están en distintos bloques (A-C, A-D, B-C y B-D). Consecuentemente, en base a éste arreglo no se puede determinar cual de los 4 genotipos podría ser el más deseable.

Ahora, considere el caso cuando un tercer genotipo (C) se distribuye en cada uno de los bloques junto a otros (A y B) que ocurren solo una vez:

De acuerdo a este arreglo, los genotipos A y B que ocurren en diferentes bloques pueden ser comparados, esto es debido a que el tercer genotipo (C) hace el papel de referencia entre los genotipos (A y B) y permite extraer la diferencia entre los bloques. Sin embargo, el grado de precisión de ésta comparación es menor (más del 40 %) que cuando los genotipos se distribuyen en el mismo bloque (A-C), esto es debido a que la comparación entre A y B es posible solo en forma indirecta sobre la referencia del tercer genotipo. Considere los genotipos A y C (ó B y C), que ocurren en el mismo bloque. La diferencia entre las medias de estos genotipos se estima con un error estándar de:

Genotipos dentro el mismo bloque:

Mientras, la diferencia entre las medias de los genotipos A y B, que ocurren en distintos bloques, se estima en forma indirecta sobre la base del tercer genotipo C como (A–C) – (B–C) = A – B, con un error estándar de:

Genotipos en diferentes bloques:

Si se distribuyen los genotipos A y B en distintos bloques, cada uno junto a dos terceros genotipos (C y D):

Estos genotipos pueden ser comparados sobre la base de los dos terceros genotipos C y D como:

con un error estándar de:

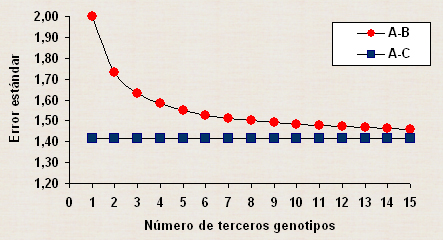
Lo cual demuestra que cuando se distribuyen dos terceros genotipos en cada bloque, el error estándar de la diferencia de medias entre genotipos ubicados en distintos bloques disminuye en más del 20 % que cuando se tenia solo un tercer genotipo. Además, sobre la variación de los efectos de los terceros genotipos en los distintos bloques y entre unidades experimentales, se puede estimar la varianza entre los bloques y de los residuales que hacen posible el ajuste de las medias y la estimación de los errores estándar.

En general, se puede demostrar que cuando el número de terceros genotipos incrementa en cada uno de los bloques, el error estándar de las diferencias entre genotipos (A-B) que ocurren en distintos bloques disminuye (Figura 1), alcanzando una mayor similitud con el error estándar de las diferencias entre medias de genotipos (A-C) que ocurren en el mismo bloque. Sin embargo, la disminución del error estándar es cada vez más pequeña a partir de tres o cuatro terceros genotipos. Estos resultados sugieren que para realizar comparaciones precisas entre genotipos en distintos bloques se puede utilizar entre tres y cuatro terceros genotipos, lo cual dependerá del cultivo, carácter de interés, del ambiente donde se desea desarrollar la investigación y de la precisión ganada con la adición de más terceros genotipos en relación al costo.

En base a los resultados obtenidos, el diseño experimental se puede desarrollar de la siguiente manera, los nuevos genotipos se distribuyen aleatoriamente en diferentes bloques. Simultáneamente, tres o cuatro genotipos (que pueden ser variedades testigo) que disponen de abundante semilla o material vegetal, se ubican al azar en cada bloque junto con los nuevos genotipos. El número de nuevos genotipos en cada bloque dependerá del tamaño de bloques que se pueden desarrollar en cada situación.

Asumiendo que A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S y T son los nuevos genotipos, X, Y y Z son los terceros genotipos y los bloques pueden agrupar ocho unidades experimentales homogéneas, el diseño experimental propuesto resultaría como sigue:

Análisis estadístico

Los datos de cada una de las variables de respuesta que se pueden considerar, de acuerdo a los objetivos de una investigación, previa verificación o aproximación mediante transformaciones a los supuestos -principalmente distribución normal y homogeneidad de varianzas- se analizan de acuerdo al siguiente modelo estadístico:

Y_ij = µ + ß_i + τ_j + ξ_ij

donde:

En base al modelo estadístico indicado, se realizan análisis de varianzas para probar hipótesis acerca de los efectos fijos y estimar componentes de varianza para los efectos aleatorios considerados en el modelo, de acuerdo a la teoría de los modelos mixtos (Searle et al., 1992) utilizando el PROC MIXED de SAS (SAS Institute, 2000 ®) ó algún programa estadístico equivalente. Las estimaciones de las varianzas de bloques y los residuales se logran únicamente sobre los efectos de los terceros genotipos; sin embargo, estos resulta dos son aplicables de igual manera a los nuevos genotipos, de acuerdo al supuesto de homogeneidad de varianzas definido en el modelo estadístico. Esto permite que las medias y diferencias entre medias de los nuevos genotipos sean estimadas y ajustadas con sus respectivos errores estándar, haciendo posible las pruebas de hipótesis acerca de estos parámetros.

Ejemplo de aplicación

Para demostrar la aplicación del diseño experimental desarrollado y evaluar su eficiencia, se considera la evaluación de dos conjuntos de líneas de arveja desarrolladas en Centro de Investigaciones Fitoecogenéticas de Pairumani (CIFP), 174 derivadas de la cruza entre Pea51-98-43 y Pea52-98-43 y 132 desarrolladas de la cruza entre Pea52-98-43 y Pea8-98-4. Cada grupo de 12 distintas líneas fueron distribuidas aleatoriamente en bloques de 15 unidades experimentales. Al mismo tiempo, dos variedades, Pairumani-1 (P-1) y Pairumani-3 (P-3) de usos comerciales y considerados como testigos y la línea M-2 que disponen de suficiente cantidad de semilla fueron ubicadas al azar entre las líneas en cada uno de los bloques. La unidad experimental fue un surco de un metro de largo y espaciado a 45 cm de los otros. Esta investigación se llevó a cabo en las propiedades del CIFP durante el periodo agrícola 2002/2003. Una parte del experimento se esquematiza de la siguiente manera:

En cada unidad experimental, se evaluaron la incidencia de la oidiosis en una escala de 0-5, rendimiento de grano (kg/ha), longitud de vaina (cm), peso de 100 semillas (g) y vigor (capacidad productiva y apariencia). Los datos obtenidos de cada grupo de líneas separadamente, previa verificación de la distribución normal y homogeneidad de varianzas, fueron analizados de acuerdo al siguiente modelo estadístico,

Y_ij = µ + ß_i + τ_j + ξ_ij

donde:

i = 1,2,..., 15 (11) bloques,
j = 1,2,...,174 (132) líneas

Los efectos de bloques y residuales se consideraron aleatorios y NIID(0,σ²_b) y NIID (0,σ²_e), respectivamente. En base al modelo estadístico, se realizaron estimaciones de componentes de varianza, errores estándar para las diferencias entre medias de líneas que ocurren en el mismo o en diferentes bloques y entre líneas con los testigos. Todos estos análisis fueron llevados a cabo utilizando el PROC MIXED de SAS (SAS Institute, 2000 ®).

Resultados y discusión

El uso de las variedades Pairumani-1 y Pairumani-3 y la línea M-2 como terceros genotipos (testigos) permitió estimar las varianzas entre bloques y de los residuales para cada una de las cinco características y en las dos cruzas (Tabla 1), las mismas, bajo los supuesto de que cada observación se distribuye con los mismos parámetros, son aplicables a las líneas que han sido evaluadas con una sola repetición. Adicionalmente, las estimaciones de los componentes de varianza para cada una de las características no difieren significativamente entre cruzas, consecuentemente, el diseño experimental propuesto hace posible no solamente la evaluación de líneas de arveja con una sola repetición, sino también permite realizar comparaciones entre ellas.

Tabla 1. Componente de varianza estimadas para diferentes características de líneas de arveja derivadas de dos cruzas.

Cruza	Parámetro	Rendimiento t/ha	Longitud vaina (cm)	Peso 100 semillas (g)	Vigor	Oidiosis
2x1		0.1125	0.0873	0.6508	0.0000	0.0333
		0.2019	0.1174	5.4222	0.7302	0.7413
2x4		0.1180	0.0000	0.0000	0.0000	0.0000
		0.1378	0.1830	2.7152	0.2182	1.6061

1 = Pea52-98-43, 2 = Pea51-98-43 y 4 = Pea8-98-4

Los errores estándar estimados para las cinco características entre líneas de las dos cruzas distribuidas en el mismo y en diferentes bloques y entre líneas con un testigo (Tabla 2) demuestran que el diseño experimental desarrollado no solamente permite comparar genotipos distribuidos en un mismo bloque, sino también, entre genotipos ubicados en distintos bloques. Sin embargo, estas comparaciones no tienen el mismo nivel de precisión. Los errores estándar entre líneas distribuidas en diferentes bloques son los más altos, pero no difieren significativamente entre líneas que ocurren en el mismo bloque (entre 2 a 11 %). Estos resultados demuestran que las comparaciones entre los nuevos genotipos que se han distribuido en el mismo o en diferentes bloques se logran con aproximadamente el mismo nivel de precisión.

Tabla 2. Errores estándar estimadas para la diferencia entre medias correspondientes a distintas características entre líneas de arveja derivadas de dos cruzas.

1 = Pea52-98-43, 2 = Pea51-98-43 y 4 = Pea8-98-4

Para las comparaciones entre líneas con los testigos, los errores estándar son más bajos y ocurre de la misma manera con las líneas que se ubican en el mismo o en diferentes bloques, lo cual era de esperar ya que cada una de las líneas se distribuyeron junto con cada uno de los testigos en el mismo número de veces y los testigos se repiten en cada uno de los bloques. Estos resultados sugieren que las comparaciones entre los nuevos genotipos con los testigos, que es lo que comúnmente práctica el mejorador, son más precisas que entre genotipos ubicados en el mismo o en distintos bloques. Consecuentemente, las selecciones realizadas de los nuevos genotipos en relación a los testigos (terceros genotipos) se lograrán con la mejor confiabilidad.

Los resultados similares alcanzados sobre la base de las cinco características entre los dos conjuntos de líneas de arveja derivadas de dos cruzas diferentes demuestran que el diseño experimental propuesto es muy efectivo en comparar no solamente genotipos con los testigos (terceros genotipos), sino también entre genotipos distribuidos en el mismo o distintos bloques. Además, esta eficiencia podría todavía ser mejorado sí se adicionan mayor número de terceros genotipos o estableciendo bloques de unidades experimentales más homogéneas. Encontrar un tamaño ideal de la unidad experimental podría también mejorar la precisión de las estimaciones, aunque en muchos casos esto esta limitado por la disponibilidad de recursos como semilla o terreno. La adición de más terceros genotipos debe ser considerada en cada cultivo, en cada condición ambiental y de penderá principalmente de la precisión ganada en relación al consto que podría significar esta adición.

Conclusiones

Se desarrolló el diseño experimental que consiste en distribuir aleatoriamente las nuevas líneas en diferentes bloques, las mismas son acompañadas con tres o cuatro variedades (testigos) en cada bloque. El diseño experimental permitió estimar componentes de varianza de bloques y los residuales, los mismos fueron importantes para ajustar y comparar con aproximadamente el mismo nivel de precisión medias de líneas en el mismo o diferentes bloques y con los testigos.

Referencias

FEHR, N. R.1993. Principies of cultivar development. Theory and technique. Department of Agronomy, Iowa State University. Ames, Iowa, USA. pp. 315-438.

MALM, N. R. and K. O. RACHIE. 1971. The setaria millets; a review of the world literature. S. B. 513. University of Nebraska College of Agriculture. Lincoln, Nebraska, USA. pp. 7-12.

SAS INSTITUTE. 1999. SAS/STAT User’s guide. Version 8, 1^st ed. SAS lnst., Cary, North Caroline, USA. pp. 2083-2226.

SEARLE, S. R., G. CASELLA, and C. E. McCULLOCH. 1992. Variance components. John Willey & Sons, Inc. lthaca, New York, USA. pp. 258-289.

Apéndice

El programa general de SAS ® para analizar los datos de los experimentos de acuerdo al diseño experimental desarrollado se desarrolla únicamente sobre la base del PROC MIXED y consiste en lo siguiente: