¹Torrico R., ²Rojas J.

1. Profesora, Jefe de Depto. Fitotecnia FCAP-UMSS

2. Tesista

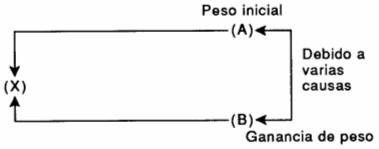
La variedad de cebolla "Roja Criolla", es la más cualitativa en Bolivia, su difusión abarca los valles centrales, valles mesotérmicos y altiplano.

El departamento de Cochabamba aporta el 44% de la producción nacional con un rendimiento medio de 7.84 t/ha, superior al promedio nacional. Estudios realizados por el IBTA-GTZ (1987), reportan a la cebolla como un cultivo de baja rentabilidad.

Otro factor que determina los bajos rendimientos es la incidencia de la enfermedad ocasionada por el hongo Peronospora destructor (Berk), conocida en el medio como "camanchaca".

Las razones anteriores inducen a iniciar un proceso de mejoramiento genético con los siguientes fines: elevar el rendimiento y seleccionar aquellos genotipos con resistencia a la camanchaca en base al método de mejoramiento de medios hermanos, tomando como criterios de selección aquellos caracteres que tienen efecto directo sobre el rendimiento.

Los métodos de mejoramiento en cebolla según Casseres (1984), han incluido selección masal, o endocría seguida por mezclas de líneas probadas, otro método es por hidridación; la androesterilidad descubierta en 1925 en el cultivar Italian Read 13-53, facilitó el proceso de la formación de híbridos.

Gardner (1961), utilizó un esquema que permite un cierto control sobre la heterogeneidad del suelo. Se trata básicamente de dividir el lote de selección en parcelas o estratos, procediendo a la selección en cada estrato independientemente de los demás. Cada estrato representa, por tanto, una unidad ambiental diferente.

Ángeles (1961), menciona que al efectuar la selección masal en una población, se pretende cambiar su media, esto es, cambiar la frecuencia de los genes que afectan al atributo en cuestión, siendo este cambio de la media poblacional proporcional a la varianza genética aditiva presente en dicha población. Este tipo de selección opera exclusivamente en los padres y de ellos se predice el comportamiento que va ha tener la descendencia.

Mariotti (1986), dice que, sin duda la selección dirigida es el procedimiento más eficaz para impulsar el progreso genético, aunque quizás sea también la instancia más crítica en el proceso del mejoramiento genético de las plantas.

Este autor, además indica que mediante la selección el fitotecnista pretende conservar los mejores genotipos de una población y descartar los mediocres o pobres partiendo de una apreciación de los rasgos fenotípicos individuales, si la selección impuesta a la población ha sido eficiente respecto a las características que persigue el mejoramiento tendrá luego un cambio drástico de las frecuencias genéticas de los genes determinantes de las características en cuestión y de otras asociadas con ellas.

Claure (1980), indica que el efecto básico de la selección es cambiar el arreglo de las frecuencias génicas de la población, y estos cambios estarán determinados por:

a) La proporción de los individuos que serán seleccionados dentro de una población (P) o presión de selección.

b) La varianza fenotipica de la población (σ²F), y

c) La heredabilidad del carácter (h²)

Stansfield (1981), por su parte, indica que si la heredabilidad de un carácter elevada, logrará progreso al seleccionar de una gran cantidad de individuos aquellos animales o vegetales que sobresalgan del resto fenotípicamente y conforme declina la heredabilidad de un carácter; de la misma manera declina la posibilidad de lograr un progreso en el mejoramiento de la población.

Falconer (1970), indica que la respuesta a la selección (R) significa la diferencia del valor fenotípico medio entre la descendencia de progenitores seleccionados y la generación paternal antes de la selección, y la conexión entre la respuesta y el diferencial de selección (D) proviene directamente del significado de heredabilidad (h²), de la siguiente manera:

R = (h2)D

donde:

R = respuesta ala selección

h² = heredabilidad del carácter

D = diferencial de selección.

Este mismo autor, proporciona un medio de predicción basado en observaciones realizadas únicamente en los individuos de la generación paternal, antes de la selección. Su validez descansa en la obtención de una estima confiable de h² usando el parecido entre parientes y la veracidad de la identidad:

bop = h2

donde: bop = regresión de progenie sobre progenitor

Finaliza indicando que existen dos métodos disponibles para el mejorador para mejorar la tasa de respuesta a la selección: uno aumentando la h² y el otro reduciendo la proporción seleccionada, y así aumentando la intensidad de selección (i), donde la ecuación de respuesta puede expresarse de la siguiente manera:

R = i * f h2

donde:

i = intensidad de selección

f = desviación fenotípica

En 1923 Wright, citado por Li (1968), postula la teoría denominada "los coeficientes de paso o de sendero". La finalidad primordial de esta teoría, dice este autor, consiste en realizar un análisis estadístico de causa y efecto de variables que estén correlacionadas. Presenta un ejemplo sencillo para definir los coeficientes de sendero.

Donde las flechas señalan la dirección de la influencia y de hecho conectan la causa con el efecto, este fenómeno denominó "sendero"; el valor numérico calculado que mide la influencia directa que ejerce una variable sobre otra, es el coeficiente de sendero, que se define como:

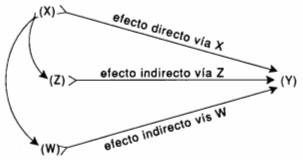
Es decir que el coeficiente de sendero Px:A (desde A hasta x), es ¡a_l relación entre la desviación estándar de x debida a A y la desviación estándar total de x.

Mosqueda y Molina (1973), determinaron en papaya (Carica papaya L.), que el peso del fruto de posición media de la planta es un buen indicador. del peso promedio de los frutos producidos por una planta. Usando el método de coeficientes de sendero de Wright determinaron que el número de frutos por planta y la anchura máxima del fruto son los componentes de rendimiento más importantes entre los 14 componentes analizados. Estos investigadores sugieren la selección individual a través del número de frutos por planta en vez de realizar selección directa para rendimiento, puesto que el número de frutos tiene mayor heredabilidad y varianza genética potencial en relación al rendimiento.

Alba, et al. (1979), aplicando el método de los coeficientes de sendero en el estudio de 4 componentes de rendimiento (número de días hasta la floración, altura de planta, diámetro del capítulo y peso de mil granos), en 16 híbridos y una variedad de red internacional FAO de girasoles; encontraron que el rendimiento de semilla influye grandemente en el rendimiento de aceite, y que el contenido de aceite mostró una acción moderada sobre la misma. Asimismo la producción de aceite y el contenido de aceite de las semillas están afectadas negativamente por la altura de planta y el diámetro del capítulo, en cambio el número de días hasta la floración ejerce un fuerte efecto directo sobre el contenido de aceite.

Wong (1980), citado por Argots (1986), señala que los coeficientes de sendero como técnica de selección de componentes de rendimiento son de gran utilidad ya que excluye otros caracteres a los cuales se les atribuye una relación importante con el rendimiento.

Mariotti (1986), indica que este procedimiento permite descomponer la correlación entre un componente (X) y el producto final, por ejemplo el rendimiento (Y), en un efecto "directo" de X sobre Y y en efectos "indirectos" de X sobre Y, los que se hacen efectivos por vía de la relación de X con otros componentes de Y (Z, W, etc.). Esta relación funcional se puede describir esquemáticamente de la siguiente manera:

El componente (X), según este autor, puede determinar un efecto "directo" sobre (Y), el que puede ser modificado por efectos indirectos vía otros componentes de (Y) también asociados con (X). De tales relaciones funcionales deriva el valor del coeficiente de correlación simple fenotípica o genotípica rXY.

Este autor, indica además, que el efecto "directo" puede interpretarse como una correlación parcial entre X e Y, una vez excluidos los efectos de W y Z (rXY. ZW). En el supuesto de independencia entre X, Z y W resultará que rXY.ZW - rXY.

El presente trabajo se llevó a cabo en la Estación Experimental "La Tamborada", dependiente de la Facultad de Ciencias Agrícolas y Pecuarias de la UMSS, situada a los 17° 23' de latitud Sur y 66° 10' de longitud Oeste del meridiano de Greenwich, a 2.570 msnm, con clima templado, sin un cambio térmico invernal bien definido, semi seco en otoño, y con un invierno y primavera secos, con una temperatura media anual de 16.5° C y una temperatura mínima media de 7.6° C.

La implantación del ensayo fue realizada en los predios de la estación Experimental de la Facultad de Ciencias Agrícolas y Pecuarias en terreno franco, utilizando la variedad Roja Criolla, variedad de ciclo intermedio, de color rojizo a morado y sabor fuerte, con forma y tamaño de bulbos variables.

La implantación del experimento fue realizado utilizando plantas de 45 días y aproximadamente 20 cm de altura. El transplante fue realizado en surcos separados a 40 m a una distancia de 10m. entre planta y planta, dando una densidad de 25.000 plantas/ha.

Durante el desarrollo de las plantas, se suministró riego de acuerdo a requerimientos de cultivo; la parcela de selección recibió una escarda a los 30 días del transplante y dos aporques, a los 50 y 90 días después del transplante.

La fertilización fue realizada utilizando 15-15-15 y Urea en una cantidad equivalente a 60-40-40 kg/ha de N P₂0₅ y K₂O respectivamente; la aplicación fue realizada en dos oportunidades: el fertilizante 15-15-15 a razón de 40-40-40 durante la primera escarda y el resto de Nitrógeno 20-0-0 durante el primer aporque.

Durante este período se controló el ataque del hongo Pernospora destructor (Bark); mediante aplicaciones de Clorotalonil.

Llegado el momento de la cosecha, para la selección de plantas se siguió el método de selección masal estratificado, Marquez (1985), dando un total de 70 sub lotes, en los que se cosecharon solamente aquellas plantas que tenían competencia completa. Como resultado de esta operación se obtuvieron 4.100 plantas, en las que posteriormente se determinaron: el peso del bulbo, la altura de planta, peso del follaje, altura del bulbo, diámetro de bulbo, diámetro de cuello de las plantas y volumen del bulbo.

Estandarización de datos para poder realizar las comparaciones entre los distintos caracteres medidos, se utilizó la siguiente fórmula:

z = (x - X)/ S

donde:

z = Valor del dato estandarizado

x = Valor real del dato

X = Media general del carácter fenotípico

S = Desviación estándar del carácter fenotípico

La determinación misma del coeficiente de peso se realizó utilizando la siguiente metodología:

- Se resolvió el sistema de ecuaciones detallado en el siguiente cuadro, recurriendo. el álgebra matricial; sistema que nos permite hallar el coeficiente de regresión parcial, que no es nada más que un indicador del número de unidades que se espera cambia la variable dependiente por cada unidad de cambio de la variable independiente. Se tomaron como variables independientes el peso de follaje (x2), altura de planta (x3), altura de bulbo (x4), diámetro de bulbo (x5) y diámetro de tallo (x6) y, como variable dependiente el peso de bulbo (Y) (rendimiento).

El vector solución (X), contiene los coeficientes de regresión parcial. Algebraicamente es igual:

X = A^-1 H

donde:

X = Es el vector que contiene el valor de las incógnitas.

A^-1 = Es la inversa de la matriz.

H = Es el vector que contiene las igualdades de la matriz.

Una vez hallados los coeficientes de regresión múltiple se procedió a la "estandarización" de los mismos para obtener por resultado el efecto directo de la variable en cuestión sobre el rendimiento.

Como resultado del análisis de los datos de los sub-lotes como un modelo de clasificación de doble entrada, se tiene el siguiente cuadro para peso de bulbo.

A partir del cuadro anterior, los valores obtenidos para la varianza fenotípica, genética y la heredabilidad son los siguientes:

Varianza genotípica 1313.397

Varianza genética 392.561

Heredabilidad en el sentido amplio 0.298

Se observa que el valor de la heredabilidad en el sentido amplio, para el peso de bulbo, presentó un valor medio de acuerdo a la clasificación de Stansfield (1970).

Para las demás variables los cuadrados medios calculados y las heredabilidades, se presentan en el cuadro, donde se observa que el peso follaje, altura de planta y diámetro cuello presentan heredabilidades altas de 0.659 a 0.509. Por otro lado se observa que diámetro bulbo presentó la heredabilidad más baja con 0.259 y volumen de bulbo tiene una heredabilidad semejante al de peso bulbo, de 0.318, con el cual está estrechamente correlacionado.

El cuadro presenta los resultados del análisis de causa y efecto, para la variable diámetro de bulbo respecto al rendimiento, presentando un efecto directo alto 0.7541.

En la figura 1, se puede observar esquemáticamente el efecto directo y efectos indirectos de esta variable sobre el rendimiento.

En orden descendente los efectos indirectos son: vía altura de bulbo 0.1133, vía diámetro cuello 0.024, vía altura de planta 0.007 y, vía peso follaje 0.006.

Al analizar el rendimiento (Y) versus diámetro cuello (x6), se tuvo que diámetro tallo presentó un efecto directo relativamente bajo de 0.1066.

El efecto directo y los efectos indirectos de este carácter sobre el rendimiento, se pueden observar gráficamente en la figura 2.

Por orden de importancia los efectos indirectos por las diferentes vías son: vía diámetro de bulbo 0.1742, vía altura bulbo 0.079; vía altura planta 0.0212, vía peso follaje 0.010.

Al analizar los coeficientes de sendero se nota que diámetro de bulbo y altura e bulbo son dos componentes particularmente importantes en este trabajo, por que de acuerdo al grado de relación con el rendimiento se podrá definir la forma más adecuada de bulbo. Diámetro bulbo presenta un efecto directo más alto con relación a altura de bulbo y los efectos indirectos vía esta variable (diámetro bulbo) también muestran valores altos; esto hace suponer que seleccionado bulbos de forma achatada se tendrá más éxito en el incremento del rendimiento de la variedad Roja Criolla.

El carácter altura de bulbo presentó un coeficiente de correlación relativamente alto de 0.674, y efecto directo también alto (segundo en importancia) de 0.2127; que representa el 31.58% de este coeficiente.

El valor elevado del coeficiente de correlación, posiblemente sea debido a efectos indirectos elevados, especialmente por vía diámetro bulbo con un valor de 0.4019, que representa el 59.69%.

Las demás vías de efecto indirecto presentaron valores bajos, así, vía diámetro tallo se tuvo el 5.9% del coeficiente de correlación; vía altura planta 1.88%; y vía peso de follaje 0.89% del coeficiente de correlación.

La altura de bulbo fue el segundo carácter en importancia, de acuerdo a su efecto directo sobre rendimiento, después del diámetro de bulbo.

Por otra parte, 0,906 el valor del coeficiente de correlación entre diámetro ,de bulbo y el rendimiento (peso de bulbo) y 0.7541 el valor del efecto directo de este sobre el peso de bulbo, que representa el 83.295 del coeficiente de correlación.

El valor de este efecto directo es el mayor de todas las variables estudiadas, en consecuencia, este carácter sería considerado como un componente importante del rendimiento.

Los efectos indirectos por las demás vías presentan valores relativamente bajos, inferiores en todos los casos al valor del efecto directo.

De acuerdo con los efectos directos e indirectos sobre el rendimiento de los distintos componentes y las respectivas heredabilidades estimadas, se seleccionaron bulbos de mayor diámetro con la esperanza de tener una mejor respuesta a la selección.

El porcentaje de respuesta teórica a la selección masal fue de 10%, que se puede considerar elevado, consecuencia de la gran variabilidad del cultivar por una parte y la heredabilidad en sentido amplio utilizada para el cálculo de la respuesta; lo que significa que se tendrá tal magnitud de respuesta solo si la varianza genética es debida en su totalidad a efectos aditivos.

Falconer (1970), al respecto recomienda que la respuesta calculada en base a la heredabilidad en el sentido amplio; debe ser tomada con cautela puesto de que existe generalmente efectos de genes con acción dominante y epistática, que en algunas oportunidades hacen que se sobreestime la respuesta a la selección masal.

De tos resultados obtenidos se puede deducir que, volumen bulbo y diámetro de bulbo fueron los que presentaron mayor correlación con el rendimiento, con coeficientes de 0.977 y 906 respectivamente, lo que demuestra una alta relación entre estos caracteres; además, muestran alta similitud en los demás estadísticos (media, varianza, etc.). En consecuencia, el volumen de bulbo también podría considerarse como un indicador del rendimiento.

El tercer carácter, por orden de importancia, correlacionado con el rendimiento fue altura de bulbo, (r = 0.677). El coeficiente de correlación de estas dos variable (altura de bulbo y diámetro de bulbo) es de 0.533. Este hecho tiene particular importancia cuando se trata de uniformizar el bulbo.

Correlaciones elevadas entre las variables independientes presentan diámetro de bulbo y volumen bulbo (r = 0.903).

Fue establecido un lote de selección masa) estratificado con la variedad de Cebolla Roja Criolla en la que fueron seleccionadas todas las plantas competitivas, se tomaron datos de peso de follaje, altura de planta, altura de bulbo, diámetro del cuello de la planta, diámetro de bulbo, peso de bulbo y volumen de bulbo; con los que se realizó un análisis de correlación y se determinaron los coeficientes de sendero para tener un criterio de selección en estos caracteres.

Los análisis mostraron que caracteres con efectos directos en el rendimiento son diámetro de bulbo y altura de bulbo; tomando estos criterios de selección fueron seleccionadas el 10% de las plantas competitivas.