Proyecto Fertilizantes, IBTA-FAO, Cochabamba, Casilla 3299.

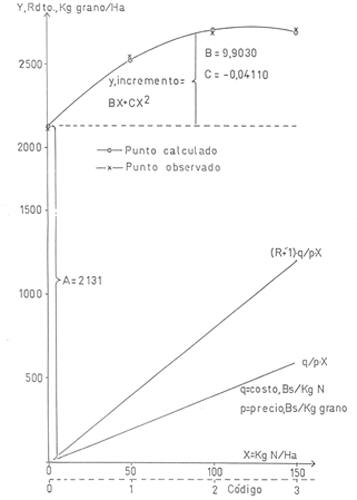
La respuesta de plantas a niveles crecientes de un nutrimento tal como N, P ó K puede describirse con curvas, véase la Gráfica 1).

La finalidad de ajustar las respuestas a niveles de nutrimentos es ante todo la de facilitar un análisis económico y para esta finalidad se destaca la ecuación cuadrática, por la facilidad de hacer dicho análisis.

La ecuación cuadrática es la siguiente:

Los coeficientes de regresión A, B Y C pueden resolverse en base a las siguientes tres ecuaciones normales:

En la ecuación (2), n es igual al número de los diferentes tratamientos. ΣX significa la suma de cada uno de los tratamientos y ΣX², la suma del cuadrado de cada uno de ellos, etc.

Para poder eliminar el término con el coeficiente A, se múltiplica la ecuación (2) con ΣX y la (3) con n, a saber:

Al substraer la ecuación (6) de la (5) se elimina los términos AnΣX y resulta la siguiente ecuación:

Multiplicando la ecuación (2) con EX2 y la (4) con n se obtiene:

Se eliminan los términos AnΣX² substrayendo la ecuación (9) de la (8) y se obtiene:

Ahora las ecuaciones (7) y (10) pueden formularse como sigue:

Para poder determinar el coeficiente C se multiplica la ecuación (16) con E y la (17) con D y substrae la (17) de la (16) y se obtiene:

Ya se puede convertir la ecuación (16) a la siguiente:

La ecuación (2) puede convertirse a la siguiente:

Datos:

Para evitar productos y sumas elevadas se hacen primero los cálculos con X en códigos:

Ahora se pueden calcular las variables D a H [ver las ecuaciones (11) a (15)]:

Para tener X en kg/ha se divide 495,15 con 50 y - 102.75 con (50X50), o sea:

En forma general dicha división se hace con la diferencia entre cada tratamiento y con dicha diferencia al cuadrado, respectivamente. Se observará que resulta más fácil hacer los cálculos manuales si se usa tratamientos equidistantes.

En la Gráfica 1 se observa la línea q/p - X, donde X es el nivel de nitrógeno, q el costo del nitrógeno en Bs/kg N y p el valor del grano en Bs/kg.

Para encontrar el nivel de X que dé la máxima utilidad se buscará una línea que sea paralela a la q/p X y tangente a la curva BX + CX², para lo cual se iguala el derivado de la línea a el de la curva:

Un agricultor no tendrá necesariamente liquidez para invertir en el insumo para lograr la máxima utilidad y resulta útil el concepto tasa de retorno marginal, R, la que indica la utilidad debida al último boliviano invertido en el insumo.

La línea de costo del insumo se multiplicará con R + 1, véase la Gráfica 1, donde sé indica tanto q/pX como (R + 1) q/p con R=1.

Si en la ecuación a (24) se substituye q/p por (R + 1) q/p se obtiene:

Habiendo determinado mediante la ejecución de ensayos la respuesta física a niveles de un nutrimento, y mediante cómputos o los cálculos indicados líneas arriba, los coeficientes B y C correspondientes resulta muy fácil para el usuario (el extensionista) actualizar los cálculos económicos.

Primero se definen la tasa de retorno marginal y el costo de fertilizantes. Además se estima el valor de la cosecha. Es conveniente usar precios a nivel de la chacra.

El costo de financiamiento se tratará en una de las siguientes formas

a) Llevar el valor de la cosecha al momento de la siembra, dividiendo el precio, P con (1 + r), donde r es el interés a pagar durante el período vegetativo. Ejemplos: 1) p = 0,40 Bs. el interés anual es de 20 % y el período vegetativo de 5 meses; por consiguiente resulta que:

r = 20/100 X 5/12 = 0,083 y 1 + r = 1,083.

b) Alternativamente se multiplicará el costo de fertilizantes con (1 + r)

Ejemplos de recomendación de niveles de nitrógeno, X:

Supuestos de respuesta física: B = 9,903 y C = -0,0411

a) Supuestos específicos: R = 0, q = 1.60 y p = 0.40

Estos tres ejemplos demuestran a la vez la importante influencia que tienen normalmente la tasa de retorno marginal y la relación del costo del insumo y el valor de la cosecha, en las recomendaciones sobre el uso del insumo. Habiendo variaciones entre localidades y entre años tanto en el costo del insumo como en el valor de la cosecha resulta importante que los extensionistas sepan realizar los cálculos según la ecuación (25) y que los investigadores, en lo posible, les entreguen la información sobre la respuesta física en una forma que permita una fácil actualización de los cálculos económicos.

Si, por interés académico se desea conocer el nivel X que dé la máxima producción se pone

R= -1 y el término (R = 1) q/p resulta cero y por consiguiente

Al tener datos de repeticiones de un ensayo o datos de varios ensayos surge la cuestión si deben usarse estos promedios. El Programa de Fertilizantes ha optado por basar los análisis de regresión en los promedios. Por consiguiente, los cálculos de regresión resultan más simples.

Supongamos que en una zona ecológica determinada se hicieron en diferentes años ensayos con niveles de nitrógeno en el cultivo de trigo, a saber:

La ecuación promedio servirá de base para formular una recomendación general para la zona ecológica en cuestión y se incluye en el promedio la variación debida a diferencias entre años, lo cual se puede justificar, aceptando que no se puede predecir al momento de fertilizar como resultará el clima.

(Modelo para Técnica de Campo)

Tres niveles equidistantes de una sola variable independiente.

Llene la Columna 1 con los datos de rendimientos correspondientes a los tratamientos respectivos y forme la suma (ΣY). Luego multiplique cada uno de los datos de rendimiento con el X correspondiente de la columna 2, ponga cada producto de la Columna 3 y forme la suma (ΣXY). En la Columna 5, ponga el producto de la Columna 1 por la 4 y forme la suma (ΣX²Y).

Llene el esquema siguiente con los valores indicados:

Luego convierta B dividiendo con la diferencia entre los niveles, y C, con el cuadrado de la diferencia. (B) ---------- / ---------- = ; (C) ---- / (----) (----) = = = = = = =

(Modelo para Técnico de campo)

- Cuatro niveles equidistantes de una sola variable independiente

Llene la Columna 1 con los datos de rendimientos correspondiente a los tratamientos respectivos y forme la suma (ΣY). Luego multiplique cada uno de los datos de rendimiento con el X correspondiente de la Columna 2, ponga cada producto en la Columna 3 y forme la suma (ΣXY). En la columna 5, ponga el producto de la Columna 1 por la 4 y forme la suma (ΣX²Y).

Llene el esquema siguiente con los valores indicados:

Luego convierta B dividiendo con la diferencia entre los niveles, y C, con el cuadrado de la diferencia. (B) ---------- / ---------- =; (C) ------ / (-----) (-----) = = = = =

Modelo para técnicos de campo.

Cinco niveles equidistantes de una segunda variable independiente:

Llene la columna 1 con los datos de rendimientos correspondientes a los tratamientos respectivos y forme la suma (ΣY). Luego multiplique cada uno de los datos de rendimiento con el X correspondiente de la Columna 2, ponga cada producto en la Columna 3 y forme la suma (ΣXY). En la Columna 5, ponga el producto de la Columna 1 por la 4 y forme la suma (ΣX²Y).

Llene el esquema siguiente con los valores indicados:

Luego convierta B dividiendo con la diferencia entre los niveles, Y C, con el cuadrado de la diferencia.