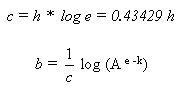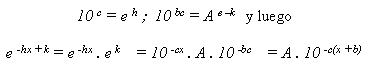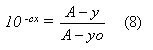|
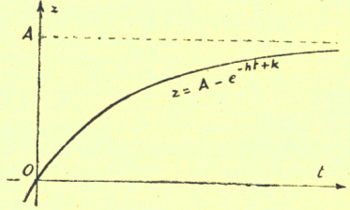
El presente trabajo tiene su origen en la discusión de una muy interesante tesis de grado recién presentada en nuestra Facultad de Agronomía , siendo su objetivo inmediato proporcionar una base teórica para los ensayos en maceta que nuestro Laboratorio de Química Agrícola se dispone a efectuar, a fin de estudiar el desarrollo vegetal en relación con el empleo de abonos, eligiendo luego las proporciones de abonos convenientes para los principales cultivos en nuestros suelos. En la preparación de esta nota hemos tenido presente la comunicación «Contribuicáo para o estudo dos métodos de Mitscherlich, Wiessmann e Neubauer» al Tercer Congreso Suramericano de Química (Río de Janeiro y San Paulo, 1937), por Saraiva, Lopes da Cruz y del Negro; pero nos alejaremos, de los métodos de demostración y de cálculo que allí se presentan, para seguir otros que nos parecen más claros y sencillos. Al estudiar hace tiempo la velocidad de las reacciones químicas autocatalíticas monomoleculares, se vio que esta resulta proporcional a la cantidad de materia todavía in descompuesta y luego se reduce progresivamente con el avance de la reacción. Traducido esto en fórmulas, llamando z la cantidad de materia descompuesta y A la cantidad total de materia que entra en reacción se tendrá que el incremento elemental dz de materia descompuesta durante el tiempo dt es proporcional, según cierto factor de proporcionalidad empírico h, a dicho intervalo de tiempo y a la cantidad A-z de materia no descompuesta todavía:
Dividiendo todo entre dt, se obtiene la fórmula siguiente, conocida bajo el nombre de ley de Wilhelmy.
tomando la derivada dz/dt el nombre de "velocidad de reacción". La integración de la ecuación diferencial (1) puede ser efectuada fácilmente como sigue: separando a las variables y cambiando de signo, tenemos:
habiéndose representado con "ln" el logaritmo natural y con k una constante arbitraria. Tomando ambos miembros como exponentes de potencias de base e, la (2) se hace:
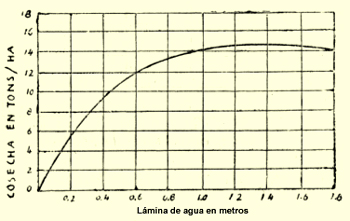
resultando luego la cantidad de materia descompuesta z representada, al variar del tiempo t, por una curva como la de arriba, curva que tiende hacia la asíntota y = A y nos demuestra claramente el reducirse progresivo de la cantidad de materia que entra en reacción. Robertson propuso a aplicar la misma fórmula (3) en el estudio del crecimiento de órganos vegetales, debiendo en tal caso z representar el tamaño que el órgano estudiado alcanza en el instante t y A su tamaño final. Efectivamente, se pudo observar que la (3) interpreta bastante bien el fenómeno, fuera de su fase inicial, que parece más bien obedecer a una ley exponencial (fórmula de Blackman ), justificándose el retardo gradual de desarrollo por la acumulación de productos asimilados o de reserva para su transformación química en el protoplasma. Por otro lado, se empezó estudiando el desarrollo vegetal, además que en condiciones naturales, también bajo la influencia de factores de desarrollo especiales, siendo talvez los experimentos más conocidos en este respecto los que la Estación Experimental Agrícola de Utah y otras en los Estados Unidos efectuaron con el objeto de determinar el efecto del riego sobre la cosecha . En dichos ensayos se proporcionan al cultivo láminas de agua siempre mayores, observándose su efecto, ya no sobre una planta aislada, sino sobre el total de la cosecha del área sembrada. Uno de tales experimentos, efectuado en Logan en cultivos de alfalfa, dio los resultados que presentamos como ejemplo en la figura 2:
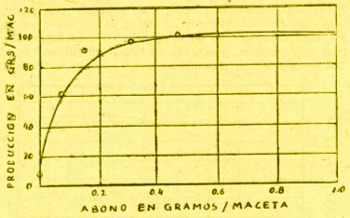
en las abscisas llevamos la lámina de agua empleada, medida en metros y en las ordenadas la cosecha, medida en toneladas por hectárea. Se puede notar que el aspecto de la curva es similar al de la figura 1; sólo se nota una tendencia a bajar por láminas mayores de 1.40 mts. aproximadamente, y esto en vista del hecho muy conocido, de que un exceso de humedad en el suelo resulta perjudicial para la vegetación, en lugar de favorecer su desarrollo . Pero el agua no es el único factor de desarrollo: temperatura, luz, fertilizantes son otros; todos estos en condiciones normales dan lugar a curvas de desarrollo del mismo tipo que las anteriores, y luego representables por la ecuación, parecida a la (3): y = A - e -hx + k (3’) donde ahora se indica con x el factor de desarrollo, con y la cosecha correspondiente y con A la cosecha máxima obtenible. La figura 3 representa una curva de desarrollo obtenida sobre cultivos de avena en maceta, en el Instituto de Química Agrícola de Río de Janeiro, al variar el factor de desarrollo «fósforo» medido en gramos por maceta, representándose la cosecha en la misma unidad de medida .
La fórmula (3') es la que se conoce bajo el nombre de ley de Mitscherlich del desarrollo vegetal. Si introducimos dos nuevas constantes b y c, definidas por las fórmulas:
donde con "log" se indica el logaritmo decimal, tendremos:
y reemplazando en la (3') obtendremos la fórmula de Mitscherlich bajo la forma más conocida:
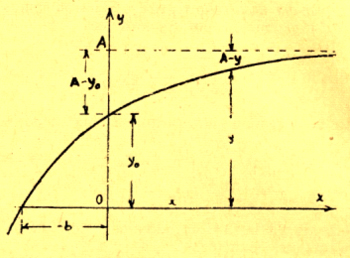
La determinación de los parámetros A, b y c, que resultan constantes en esos fenómenos que siguen estrictamente la ley de Mitscherlich, tiene que efectuarse en base a ensayos cuidadosamente llevados a cabo y promediados con métodos estadísticos. De estos se deducirán varios pares de valores (x, y) que satisfacen la (4) y llevando el experimento hasta valores muy grandes del factor de desarrollo x, se determinará también la cosecha máxima A. Reemplazados en (4) los valores así hallados, resultarán varias ecuaciones en las incógnitas b y c, de las cuales se sacarán los valores más probables de dichos coeficientes. En la práctica, podemos dar a la (4) una forma más conveniente, en base a las siguientes consideraciones. Llamado y0 la producción correspondiente al valor cero del factor de desarrollo x (ver la figura 4) tendremos de la ecuación (4): yo = A (1 - 10 -cb)) (5) y restando la (5) de la (4): y - yo = A (1 - 10 -c (x + b)) - A (1 - 10 - cb) = A (-10 -c (x + b) + 10 -cb) = -A . 10 -cb (10 -cx - 1) (6)
Por lado es por la (5): yo = A - A . 10 -cb de lo que sigue: A . 10 -cb = A-yo (7) Reemplazando en la (6), resulta: y - yo = - (A - yo) (10 -cx - 1) = - A . 10 -cx + A + yo . 10 -cx - yo o sea, simplificando: y = - A . 10 -cx + A + yo . 10 -cx = 10 -cx (A - yo) + A De esta se saca por fin: 10 -cx (A - yo) = A - y y despejando
Por intermedio de las fórmulas (7) y (8) se puede efectuar sin dificultad el cálculo de los coeficientes b y c. Para ofrecer un ejemplo de cálculo efectivo, salgamos de los datos experimentales a que se refiere la gráfica de la figura 3: se trata, como ya indicamos, de una serie de ensayos destinados a determinar el desarrollo y obtenido al variar del abono fósforo (variable x) en cultivo de avena en maceta. Los datos son los siguientes: Cantidad de fósforo en grs/ maceta 0.000 0.078 0.155 0.311 0.466 1.552 Producción observada en grs/ maceta 9.7 62.6 92.2 99.4 100.4 102.1 Además se observó que, con crecer mayormente la cantidad de abono, no se podía conseguir mayor aumento de producción, así que se puede !tomar A = 102.1 grs/ maceta. Siendo luego yo = 9.7 A = 102.1 será A- yo = 102.1 - 9.7 = 92.4
Ahora, si para c tomamos el promedio aritmético de los cuatro valores hallados, resulta: c = (4.68 + 6.26 + 4.94 + 3.89): 4 = 19.75 : 4 = 4.94.
Para comprobación, volvamos a calcular con esta fórmula valores de las cosechas correspondientes a las cantidades de abono empleadas en los ensayos. Por ejemplo por x = 0 tendremos: y = 102.1 (1 - 10 - 4.94 ´ 0.009) = 102. 1 (1 - 10 -0.0445) = 102.1 (1 - 0.902) = 102.1 ´ 0.098 = 10.0 y procediendo de manera parecida para todos los demás valores de x, llegaremos a los resultados que se detallan a continuación: Cantidad de fósforo en grs /maceta 0 0.078 0.155 0.311 0.466 0.552 Producción calculada en grs/ maceta 10.0 62.3 86.3 99.5 101.6 102.1 cuya buena aproximación con los resultados experimentales salta a la vista. Podemos luego sacar las conclusiones siguientes: - El desarrollo de los cultivos estudiados, en las condiciones del experimento, sigue en forma bastante aproximada la ley de Mitscherlich. - Queriendo expresar dicho desarrollo por una fórmula del tipo (4), se tendrá que poner A =102.1 grs/ maceta, b = 0.009, c = 4.94 (o valores que se alejen muy poco de estos), resultando luego la fórmula (9). - La fórmula (9) nos permitirá calcular el efecto de cualquier cantidad determinada de fósforo en el terreno, en todo caso práctico que, por lo que concierne a los demás factores, (tipo de cultivo, suelo, clima, riego, etc.) se pueda considerar prácticamente en las mismas condiciones que las experiencias efectuadas. Publicaciones de la Universidad Autónoma de Cochabamba, Bolivia Sobre obras de agricultura – botánica - forestalia
N°. 1. Principales características físicas de los suelos. Por el Ing. Enrique Espinosa V. Publicación No. 1; 1941. N°. 2. Contribución a la flora económica de Bolivia. Por el Dr. Martín Cárdenas. Publicación No. 2; 1941. N°. 3. Noticia histórica y clasificación de la papa boliviana. Por el Ing. Wálter Cevallos Tovar. Publicación No. 3; 1941. N°. 4. Notas preliminares sobre la, materia médica boliviana. Sinopsis de la flora médica de Bolivia. Por el Dr. Martín Cárdenas. Publicación No. 4; 1943. N°. 5. Nuevas contribuciones a la flora económica de Bolivia.por el Dr. Martín Cárdenas. Publicación No. 5; 1944. N°. 6 - 7. La Quinua. El Centeno. Por el Ing. Wálter Cevallos Tovar. Publicación No. 6 - 7; 1945. N°. 8. Modo de combatir el Ulu de la Coca y su Biología. Por Rodolfo Zischka y Martín Cárdenas. Publicación No. 8; 1947. N°. 9. Mejoramiento del maíz en los valles de Bolivia-Por el Dr. Martín Cárdenas y el Dr. Hugh C. Cutler. Publicación No. 9; 1947. N°. 11. La lucha contra los insectos dañinos a la agricultura. Por Rodolfo Zischka.- Publicación No. 11; 1948. N°. 12. Las hormigas cortadoras de hoja y su destrucción. Los piojos verdes. Por Rodolfo Zischka. Publicación No. 12; 1948. |